Коли я вперше спробував пояснити дитині, що таке висота рівнобедреного трикутника, зрозумів: шкільна теорія — це одне, а от донести сенс по-людськи — зовсім інше. Бо що ми чуємо в підручниках? «Перпендикуляр, проведений із вершини до основи…» Але як це уявити в реальному житті?
Уявімо, що ви будуєте намет. Ви забили два кілки й натягли тканину так, щоб вона з обох боків виглядала симетрично. І щоб вона стояла рівно — з’єднали її верхівку з точкою на землі по центру. Ось ця уявна “мотузка вниз” — це і є висота. Тільки в геометрії її не натягують, а проводять.
Що таке висота в рівнобедреному трикутнику і чим вона особлива
У рівнобедреному трикутнику є одна цікава риса: висота, проведена до основи, водночас є і медіаною, і бісектрисою. Це звучить складно, але означає дуже просту річ — вона ділить трикутник навпіл, причому не лише по довжині, а й по кутах. Уявіть, що ви ріжете симетричну піцу навпіл — ви автоматично і ділите її рівно, і «вказуєте» центр.
У будівництві чи кресленні такий трикутник допомагає забезпечити симетрію. Наприклад, при виготовленні даху або опор — там, де важливо, щоб ліва й права частини мали однакове навантаження.
 Як знайти висоту: проста формула і приклад
Як знайти висоту: проста формула і приклад
Пам’ятаєте теорему Піфагора? Так от, у рівнобедреному трикутнику її можна застосувати дуже зручно. Якщо a — бічна сторона, а b — основа, то формула виглядає так:
h = √(a² – (b/2)²)
Щоб не заглиблюватися у літери, візьмемо приклад. Є трикутник з бічними сторонами по 10 см і основою 12 см. Спочатку поділимо основу навпіл — буде 6. Далі:
h = √(10² – 6²) = √(100 – 36) = √64 = 8 см
Маємо готову відповідь. Без складних конструкцій і теорем. До речі, якщо основа — парне число, порахувати ще легше.
Можна тренуватись із побутовими речами. Наприклад, якщо ви маєте дві однакові дошки і хочете з’єднати їх знизу третьою — обчислити висоту можна саме так. Це допоможе не лише в задачах, а й на дачі.
Якщо ви щойно пригадали, що не раз стикалися з такою ситуацією — це гарний момент спробувати формулу на практиці.
Коли дано не всі сторони — як тоді?
Буває, що відома тільки площа і основа. Не проблема. Формула площі трикутника:
S = ½ × b × h
Із неї легко виразити висоту:
h = (2 × S) / b
Наприклад, площа 30 см², основа 10 см:
h = (2 × 30) / 10 = 6 см
Такий метод часто використовують у реальних задачах, коли площу виміряно через інші параметри. Наприклад, у будівельних кресленнях, коли вже є площа секції, але треба перевірити висоту конструкції.
А ще висоту можна знайти через тригонометрію, але для побутових і простих шкільних задач — формули через Піфагора або площу вистачає з головою.
Спробуйте застосувати обидві формули на різних прикладах — ви побачите, що вже починаєте орієнтуватися не гірше за вчителя.
Чим корисна ця висота у житті та навчанні
На перший погляд — це просто частина геометрії. Але якщо придивитися уважніше — це ключ до багатьох задач. Через неї можна:
швидко знайти площу;
поділити фігуру на дві рівні частини;
побудувати симетричну конструкцію;
розрахувати навантаження в кресленнях.
Навіть якщо ви не працюєте інженером, ця навичка знадобиться. Наприклад, щоб намалювати симетричну табличку, вирізати рівний трикутний шматок фанери або вишити геометричну фігуру на полотні.
У шкільних задачах висота часто з’являється раптово: наче все про кути, а потім — “знайти висоту до основи”. І тут формула рятує.
Не зупиняйтесь на одному прикладі. Обирайте власні задачі з життя — тоді формули оживають і запам’ятовуються самі собою.
 Коли висота стає особливою: тупокутний і гострокутний трикутники
Коли висота стає особливою: тупокутний і гострокутний трикутники
У рівнобедреному трикутнику не завжди кути однакові. Якщо кут між бічними сторонами гострий — висота буде всередині. Але якщо тупий — висота виходить за межі фігури. Це трохи ламає шаблон, але логіка залишається: ми все одно проводимо перпендикуляр до основи.
У побуті таке буває, коли ви, наприклад, відкрили кришку і тримаєте її під кутом — утворюється умовний тупокутний трикутник. Якщо хочете дізнатися висоту «накриття» — вона буде поза межами самого трикутника, але по суті залишиться його частиною.
У кресленнях або 3D-моделях іноді потрібно спеціально виносити висоту за межі фігури — щоб вона не перекривала елементи всередині. Геометрія тут цілком відповідає практиці.
Варто потренуватися з різними формами — так краще зрозуміється логіка побудови.
Висота — це не просто лінія. Це ключ до симетрії, площі, рівноваги. Вона пов’язує сторони, кути й завдання. І навіть якщо формула здається на перший погляд складною — після кількох прикладів вона стає майже інтуїтивною.
Більше практики — менше страху перед формулами. І більше розуміння, як усе це пов’язано з реальним життям.
 Як знайти висоту: проста формула і приклад
Як знайти висоту: проста формула і приклад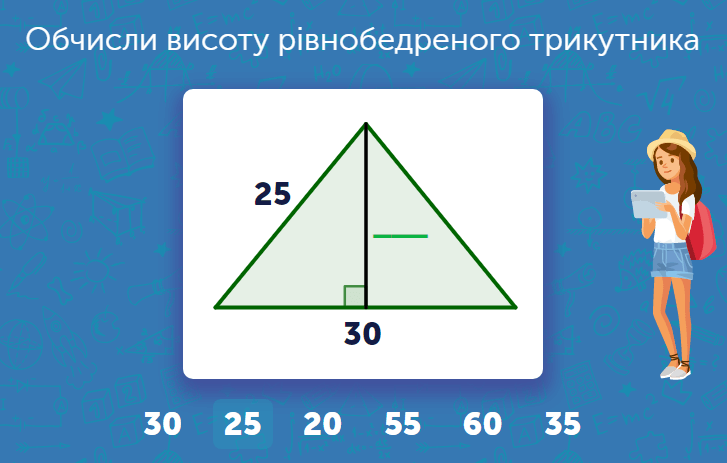 Коли висота стає особливою: тупокутний і гострокутний трикутники
Коли висота стає особливою: тупокутний і гострокутний трикутники